前言

樹(shù)是數據結構中(zhōng)的重中(zhōng)之重，尤其以各類二叉樹(shù)爲學習的難點。一(yī)直以來，對于樹(shù)的掌握都是模棱兩可的狀态，現在希望通過寫一(yī)個關于二叉樹(shù)的專題系列。在學習與總結的同時更加深入的了解掌握二叉樹(shù)。本系列文章将着重介紹一(yī)般二叉樹(shù)、完全二叉樹(shù)、滿二叉樹(shù)、線索二叉樹(shù)、霍夫曼樹(shù)、二叉排序樹(shù)、平衡二叉樹(shù)、紅黑樹(shù)、B樹(shù)。希望各位讀者能夠關注專題，并給出相應意見，通過系列的學習做到心中(zhōng)有“樹(shù)”。

1.重點概念

1.1 結點概念

結點是數據結構中(zhōng)的基礎，是構成複雜(zá)數據結構的基本組成單位。

1.2 樹(shù)結點聲明

本系列文章中(zhōng)提及的結點專指樹(shù)的結點。例如：結點A在圖中(zhōng)表示爲：

2樹(shù)

2.1 定義

樹(shù)（Tree）是n（n>=0)個結點的有限集。n=0時稱爲空樹(shù)。在任意一(yī)顆非空樹(shù)中(zhōng)：

1）有且僅有一(yī)個特定的稱爲根（Root）的結點；

2）當n>1時，其餘結點可分(fēn)爲m(m>0)個互不相交的有限集T1、T2、......、Tn，其中(zhōng)每一(yī)個集合本身又(yòu)是一(yī)棵樹(shù)，并且稱爲根的子樹(shù)。

此外(wài)，樹(shù)的定義還需要強調以下(xià)兩點：

1）n>0時根結點是唯一(yī)的，不可能存在多個根結點，數據結構中(zhōng)的樹(shù)隻能有一(yī)個根結點。

2）m>0時，子樹(shù)的個數沒有限制，但它們一(yī)定是互不相交的。

示例樹(shù)：

圖2.1爲一(yī)棵普通的樹(shù)：

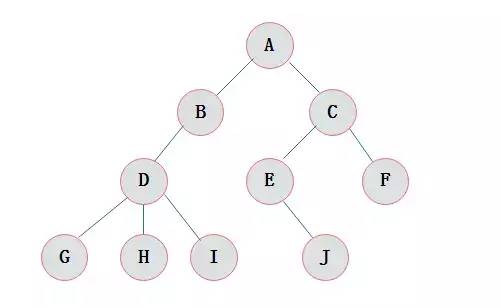
圖2.1 普通樹(shù)

由樹(shù)的定義可以看出，樹(shù)的定義使用了遞歸的方式。遞歸在樹(shù)的學習過程中(zhōng)起着重要作用，如果對于遞歸不是十分(fēn)了解，建議先看看遞歸算法

2.2 結點的度

結點擁有的子樹(shù)數目稱爲結點的度。

圖2.2中(zhōng)标注了圖2.1所示樹(shù)的各個結點的度。

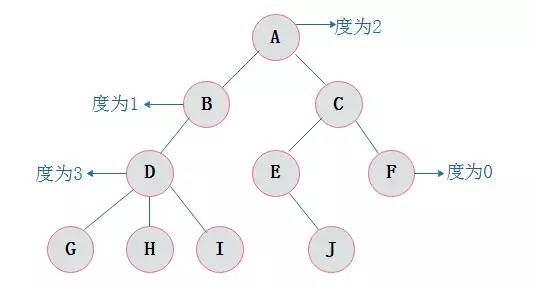
圖2.2 度示意圖

2.3 結點關系

結點子樹(shù)的根結點爲該結點的孩子結點。相應該結點稱爲孩子結點的雙親結點。

圖2.2中(zhōng)，A爲B的雙親結點，B爲A的孩子結點。

同一(yī)個雙親結點的孩子結點之間互稱兄弟(dì)結點。

圖2.2中(zhōng)，結點B與結點C互爲兄弟(dì)結點。

2.4 結點層次

從根開(kāi)始定義起，根爲第一(yī)層，根的孩子爲第二層，以此類推。

圖2.3表示了圖2.1所示樹(shù)的層次關系

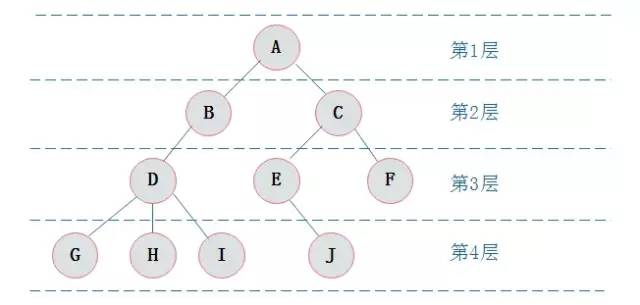
圖2.3 層示意圖

2.5 樹(shù)的深度

樹(shù)中(zhōng)結點的最大(dà)層次數稱爲樹(shù)的深度或高度。圖2.1所示樹(shù)的深度爲4。

3.二叉樹(shù)

3.1 定義

二叉樹(shù)是n(n>=0)個結點的有限集合，該集合或者爲空集（稱爲空二叉樹(shù)），或者由一(yī)個根結點和兩棵互不相交的、分(fēn)别稱爲根結點的左子樹(shù)和右子樹(shù)組成。

圖3.1展示了一(yī)棵普通二叉樹(shù)：

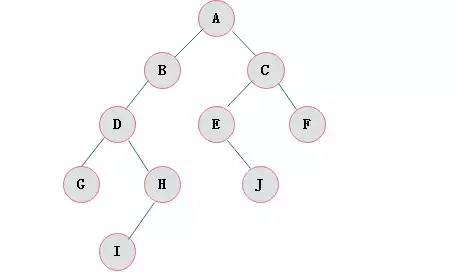
圖3.1 二叉樹(shù)

3.2 二叉樹(shù)特點

由二叉樹(shù)定義以及圖示分(fēn)析得出二叉樹(shù)有以下(xià)特點：

1）每個結點最多有兩顆子樹(shù)，所以二叉樹(shù)中(zhōng)不存在度大(dà)于2的結點。

2）左子樹(shù)和右子樹(shù)是有順序的，次序不能任意颠倒。

3）即使樹(shù)中(zhōng)某結點隻有一(yī)棵子樹(shù)，也要區分(fēn)它是左子樹(shù)還是右子樹(shù)。

3.3 二叉樹(shù)性質

1）在二叉樹(shù)的第i層上最多有2i-1 個節點 。（i>=1）

2）二叉樹(shù)中(zhōng)如果深度爲k,那麽最多有2k-1個節點。(k>=1）

3）n0=n2+1  n0表示度數爲0的節點數，n2表示度數爲2的節點數。

4）在完全二叉樹(shù)中(zhōng)，具有n個節點的完全二叉樹(shù)的深度爲[log2n]+1，其中(zhōng)[log2n]是向下(xià)取整。

5）若對含 n 個結點的完全二叉樹(shù)從上到下(xià)且從左至右進行 1 至 n 的編号，則對完全二叉樹(shù)中(zhōng)任意一(yī)個編号爲 i 的結點有如下(xià)特性：

(1) 若 i=1，則該結點是二叉樹(shù)的根，無雙親, 否則，編号爲 [i/2] 的結點爲其雙親結點;

(2) 若 2i>n，則該結點無左孩子，  否則，編号爲 2i 的結點爲其左孩子結點；

(3) 若 2i+1>n，則該結點無右孩子結點，  否則，編号爲2i+1 的結點爲其右孩子結點。

3.4 斜樹(shù)

斜樹(shù)：所有的結點都隻有左子樹(shù)的二叉樹(shù)叫左斜樹(shù)。所有結點都是隻有右子樹(shù)的二叉樹(shù)叫右斜樹(shù)。這兩者統稱爲斜樹(shù)。

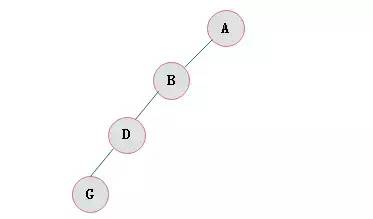
圖3.2 左斜樹(shù)

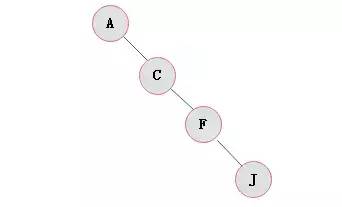
圖3.3 右斜樹(shù)

3.5 滿二叉樹(shù)

滿二叉樹(shù)：在一(yī)棵二叉樹(shù)中(zhōng)。如果所有分(fēn)支結點都存在左子樹(shù)和右子樹(shù)，并且所有葉子都在同一(yī)層上，這樣的二叉樹(shù)稱爲滿二叉樹(shù)。

滿二叉樹(shù)的特點有：

1）葉子隻能出現在最下(xià)一(yī)層。出現在其它層就不可能達成平衡。

2）非葉子結點的度一(yī)定是2。

3）在同樣深度的二叉樹(shù)中(zhōng)，滿二叉樹(shù)的結點個數最多，葉子數最多。

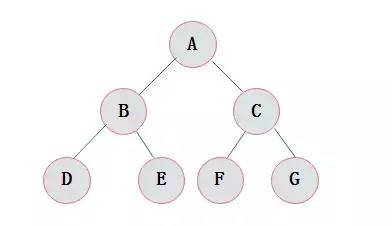
圖3.4 滿二叉樹(shù)

3.6 完全二叉樹(shù)

完全二叉樹(shù)：對一(yī)顆具有n個結點的二叉樹(shù)按層編号，如果編号爲i(1<=i<=n)的結點與同樣深度的滿二叉樹(shù)中(zhōng)編号爲i的結點在二叉樹(shù)中(zhōng)位置完全相同，則這棵二叉樹(shù)稱爲完全二叉樹(shù)。

圖3.5展示一(yī)棵完全二叉樹(shù)

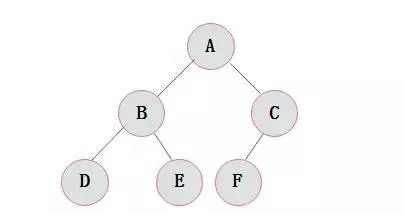
圖3.5 完全二叉樹(shù)

特點：

1）葉子結點隻能出現在最下(xià)層和次下(xià)層。

2）最下(xià)層的葉子結點集中(zhōng)在樹(shù)的左部。

3）倒數第二層若存在葉子結點，一(yī)定在右部連續位置。

4）如果結點度爲1，則該結點隻有左孩子，即沒有右子樹(shù)。

5）同樣結點數目的二叉樹(shù)，完全二叉樹(shù)深度最小(xiǎo)。

注：滿二叉樹(shù)一(yī)定是完全二叉樹(shù)，但反過來不一(yī)定成立。

3.7 二叉樹(shù)的存儲結構

3.7.1 順序存儲

二叉樹(shù)的順序存儲結構就是使用一(yī)維數組存儲二叉樹(shù)中(zhōng)的結點，并且結點的存儲位置，就是數組的下(xià)标索引。

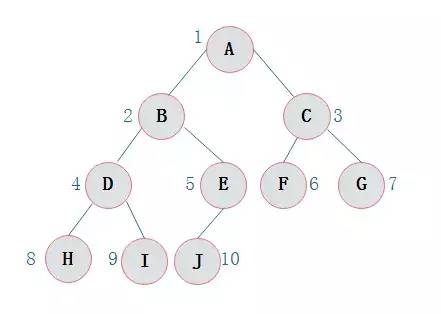
圖3.6

圖3.6所示的一(yī)棵完全二叉樹(shù)采用順序存儲方式，如圖3.7表示：

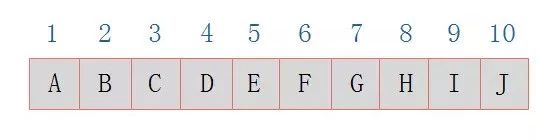
圖3.7 順序存儲

由圖3.7可以看出，當二叉樹(shù)爲完全二叉樹(shù)時，結點數剛好填滿數組。

那麽當二叉樹(shù)不爲完全二叉樹(shù)時，采用順序存儲形式如何呢？例如：對于圖3.8描述的二叉樹(shù)：

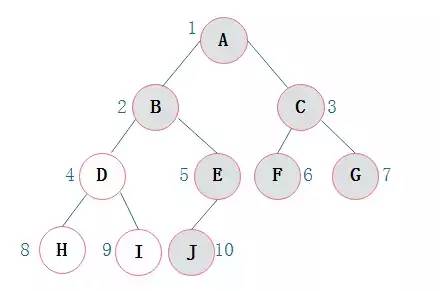
圖3.8.png

其中(zhōng)淺色結點表示結點不存在。那麽圖3.8所示的二叉樹(shù)的順序存儲結構如圖3.9所示：

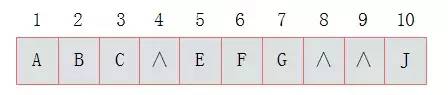
圖3.9

其中(zhōng)，∧表示數組中(zhōng)此位置沒有存儲結點。此時可以發現，順序存儲結構中(zhōng)已經出現了空間浪費(fèi)的情況。

那麽對于圖3.3所示的右斜樹(shù)極端情況對應的順序存儲結構如圖3.10所示：

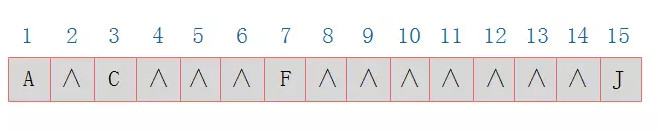
圖3.10

由圖3.10可以看出，對于這種右斜樹(shù)極端情況，采用順序存儲的方式是十分(fēn)浪費(fèi)空間的。因此，順序存儲一(yī)般适用于完全二叉樹(shù)。

3.7.2 二叉鏈表

既然順序存儲不能滿足二叉樹(shù)的存儲需求，那麽考慮采用鏈式存儲。由二叉樹(shù)定義可知(zhī)，二叉樹(shù)的每個結點最多有兩個孩子。因此，可以将結點數據結構定義爲一(yī)個數據和兩個指

針域。表示方式如圖3.11所示：

圖3.11

定義結點代碼：

typedef struct BiTNode{

    TElemType data;//數據

    struct BiTNode *lchild, *rchild;//左右孩子指針

} BiTNode, *BiTree;

則圖3.6所示的二叉樹(shù)可以采用圖3.12表示。

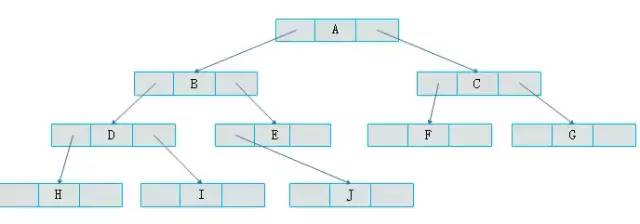
圖3.12

圖3.12中(zhōng)采用一(yī)種鏈表結構存儲二叉樹(shù)，這種鏈表稱爲二叉鏈表。

3.8 二叉樹(shù)遍曆

二叉樹(shù)的遍曆一(yī)個重點考查的知(zhī)識點。

3.8.1 定義

二叉樹(shù)的遍曆是指從二叉樹(shù)的根結點出發，按照某種次序依次訪問二叉樹(shù)中(zhōng)的所有結點，使得每個結點被訪問一(yī)次，且僅被訪問一(yī)次。

二叉樹(shù)的訪問次序可以分(fēn)爲四種：

前序遍曆

中(zhōng)序遍曆

後序遍曆

層序遍曆

3.8.2 前序遍曆

前序遍曆通俗的說就是從二叉樹(shù)的根結點出發，當第一(yī)次到達結點時就輸出結點數據，按照先向左在向右的方向訪問。

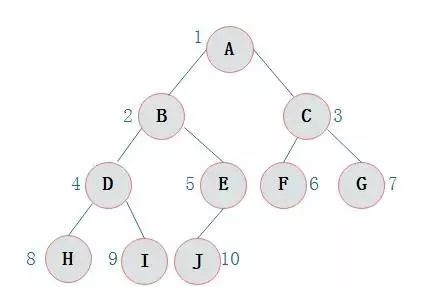
3.13

圖3.13所示二叉樹(shù)訪問如下(xià)：

從根結點出發，則第一(yī)次到達結點A，故輸出A;

繼續向左訪問，第一(yī)次訪問結點B，故輸出B；

按照同樣規則，輸出D，輸出H；

當到達葉子結點H，返回到D，此時已經是第二次到達D，故不在輸出D，進而向D右子樹(shù)訪問，D右子樹(shù)不爲空，則訪問至I，第一(yī)次到達I，則輸出I；

I爲葉子結點，則返回到D，D左右子樹(shù)已經訪問完畢，則返回到B，進而到B右子樹(shù)，第一(yī)次到達E，故輸出E；

向E左子樹(shù)，故輸出J；

按照同樣的訪問規則，繼續輸出C、F、G；

則3.13所示二叉樹(shù)的前序遍曆輸出爲：

ABDHIEJCFG

3.8.3 中(zhōng)序遍曆

中(zhōng)序遍曆就是從二叉樹(shù)的根結點出發，當第二次到達結點時就輸出結點數據，按照先向左在向右的方向訪問。

圖3.13所示二叉樹(shù)中(zhōng)序訪問如下(xià)：

從根結點出發，則第一(yī)次到達結點A，不輸出A，繼續向左訪問，第一(yī)次訪問結點B，不輸出B；繼續到達D，H；

到達H，H左子樹(shù)爲空，則返回到H，此時第二次訪問H，故輸出H；

H右子樹(shù)爲空，則返回至D，此時第二次到達D，故輸出D；

由D返回至B，第二次到達B，故輸出B；

按照同樣規則繼續訪問，輸出J、E、A、F、C、G；

則3.13所示二叉樹(shù)的中(zhōng)序遍曆輸出爲：

HDIBJEAFCG

3.8.4 後序遍曆

後序遍曆就是從二叉樹(shù)的根結點出發，當第三次到達結點時就輸出結點數據，按照先向左在向右的方向訪問。

圖3.13所示二叉樹(shù)後序訪問如下(xià)：

從根結點出發，則第一(yī)次到達結點A，不輸出A，繼續向左訪問，第一(yī)次訪問結點B，不輸出B；繼續到達D，H；

到達H，H左子樹(shù)爲空，則返回到H，此時第二次訪問H，不輸出H；

H右子樹(shù)爲空，則返回至H，此時第三次到達H，故輸出H；

由H返回至D，第二次到達D，不輸出D；

繼續訪問至I，I左右子樹(shù)均爲空，故第三次訪問I時，輸出I；

返回至D，此時第三次到達D，故輸出D；

按照同樣規則繼續訪問，輸出J、E、B、F、G、C，A；

則圖3.13所示二叉樹(shù)的後序遍曆輸出爲：

HIDJEBFGCA

雖然二叉樹(shù)的遍曆過程看似繁瑣，但是由于二叉樹(shù)是一(yī)種遞歸定義的結構，故采用遞歸方式遍曆二叉樹(shù)的代碼十分(fēn)簡單。

遞歸實現代碼如下(xià)：

/*二叉樹(shù)的前序遍曆遞歸算法*/

void PreOrderTraverse(BiTree T)

{

    if(T==NULL)

    return;

    printf("%c", T->data);  /*顯示結點數據，可以更改爲其他對結點操作*/

    PreOrderTraverse(T->lchild);    /*再先序遍曆左子樹(shù)*/

    PreOrderTraverse(T->rchild);    /*最後先序遍曆右子樹(shù)*/

}

/*二叉樹(shù)的中(zhōng)序遍曆遞歸算法*/

void InOrderTraverse(BiTree T)

{

    if(T==NULL)

    return;

    InOrderTraverse(T->lchild); /*中(zhōng)序遍曆左子樹(shù)*/

    printf("%c", T->data);  /*顯示結點數據，可以更改爲其他對結點操作*/

    InOrderTraverse(T->rchild); /*最後中(zhōng)序遍曆右子樹(shù)*/

}

/*二叉樹(shù)的後序遍曆遞歸算法*/

void PostOrderTraverse(BiTree T)

{

    if(T==NULL)

    return;

    PostOrderTraverse(T->lchild);   /*先後序遍曆左子樹(shù)*/

    PostOrderTraverse(T->rchild);   /*再後續遍曆右子樹(shù)*/

    printf("%c", T->data);  /*顯示結點數據，可以更改爲其他對結點操作*/

}

3.8.5 層次遍曆

層次遍曆就是按照樹(shù)的層次自上而下(xià)的遍曆二叉樹(shù)。針對圖3.13所示二叉樹(shù)的層次遍曆結果爲：

ABCDEFGHIJ

3.8.6 遍曆常考考點

對于二叉樹(shù)的遍曆有一(yī)類典型題型。

1）已知(zhī)前序遍曆序列和中(zhōng)序遍曆序列，确定一(yī)棵二叉樹(shù)。

例題：若一(yī)棵二叉樹(shù)的前序遍曆爲ABCDEF，中(zhōng)序遍曆爲CBAEDF，請畫出這棵二叉樹(shù)。

分(fēn)析：前序遍曆第一(yī)個輸出結點爲根結點，故A爲根結點。早中(zhōng)序遍曆中(zhōng)根結點處于左右子樹(shù)結點中(zhōng)間，故結點A的左子樹(shù)中(zhōng)結點有CB，右子樹(shù)中(zhōng)結點有EDF。

如圖3.14所示：

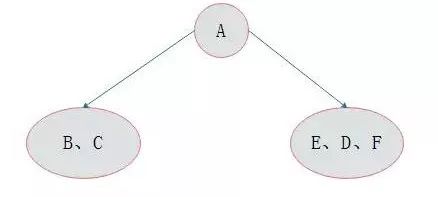
圖3.14

按照同樣的分(fēn)析方法，對A的左右子樹(shù)進行劃分(fēn)，最後得出二叉樹(shù)的形态如圖3.15所示：

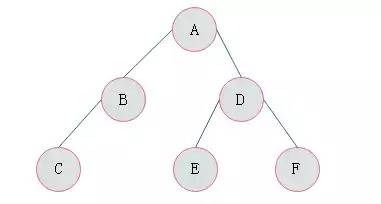
圖3.15.png

2）已知(zhī)後序遍曆序列和中(zhōng)序遍曆序列，确定一(yī)棵二叉樹(shù)。

後序遍曆中(zhōng)最後訪問的爲根結點，因此可以按照上述同樣的方法，找到根結點後分(fēn)成兩棵子樹(shù)，進而繼續找到子樹(shù)的根結點，一(yī)步步确定二叉樹(shù)的形态。

注：已知(zhī)前序遍曆序列和後序遍曆序列，不可以唯一(yī)确定一(yī)棵二叉樹(shù)。

4.結語

通過上述的介紹，已經對于二叉樹(shù)有了初步的認識。本篇文章介紹的基礎知(zhī)識希望讀者能夠牢牢掌握，并且能夠在腦海中(zhōng)建立一(yī)棵二叉樹(shù)的模型，爲後續學習打好基礎。